TIMELINE OF OUR RESEARCH
Conceptual breakthrough |
Tools development |
-
The fundamental unit of cell size in bacteria
F. Si et al., Current Biology 27, 1278–1287 (2017)
We explain the overarching quantitative principle of cell size control in bacteria. Briefly, we discovered the fundamental unit of cell size in bacteria, which remains invariant under extensive inhibition of biosynthesis. The cell size is therefore a sum of all invariant unit cells, and the resulting ‘general growth law’ predicts cell size under any growth condition. This is one of the most important results from our lab.
Read more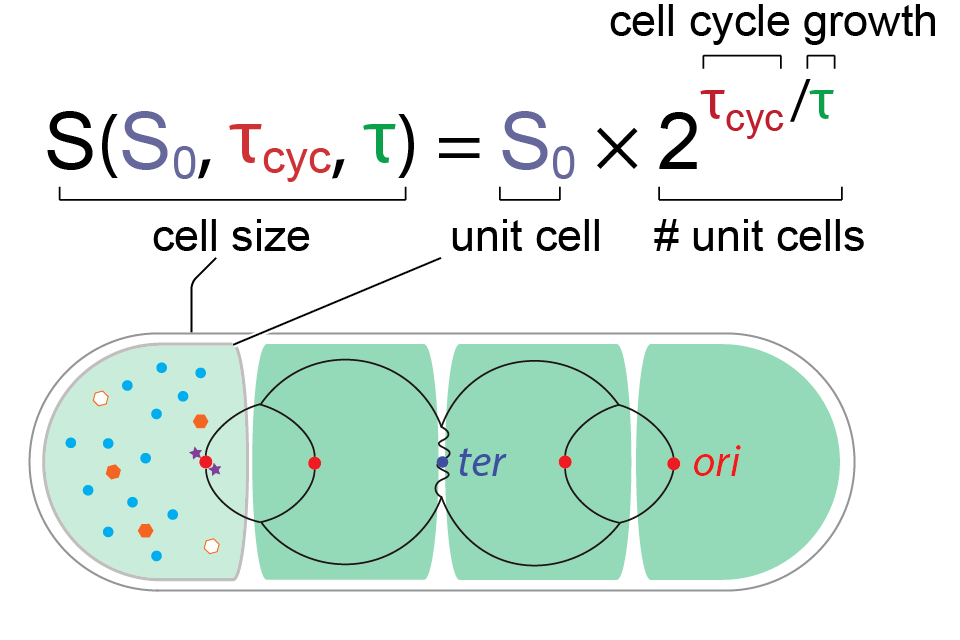
-
A tunable CRISPR interference system
X. Li et al., Scientific Reports (2016) 6, 39076.
We developed "tCRISPRi" for precise and continuous titration of gene expression with minimal leaky repression, especially suitable for physiological studies. Construction of tCRISPRi to target a new gene requires only one-step of oligo recombineering.
Read more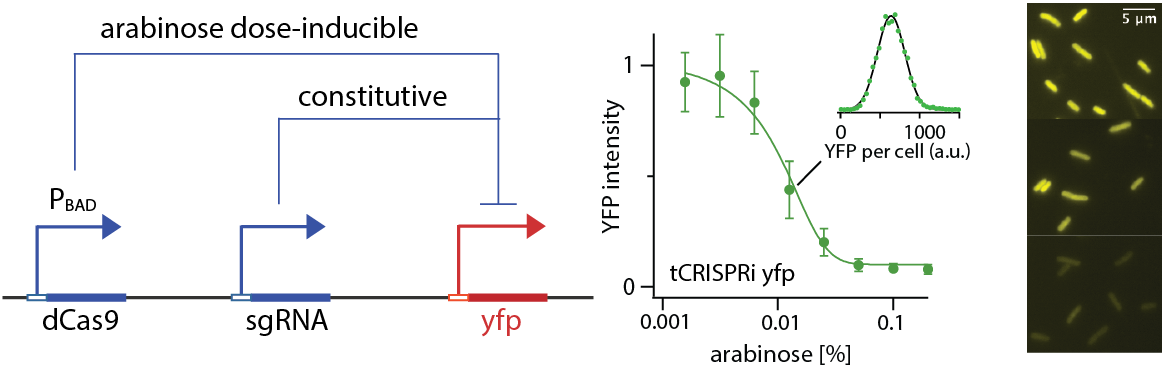
-
The adder principle of size homeostasis
S. Taheri-Araghi et al., Current Biology 25, 385–391 (2015).
S. Jun, S. Taheri-Araghi, Trends Microbiol. 23, 4–6 (2015).We discovered and introduced the notion of the “adder” principle of cell size control and homeostasis. There is interesting story what led to our discovery originally in 2012 and why we named the principle “adder.” Those curious should look at the extended version of the supplementary information.
Read more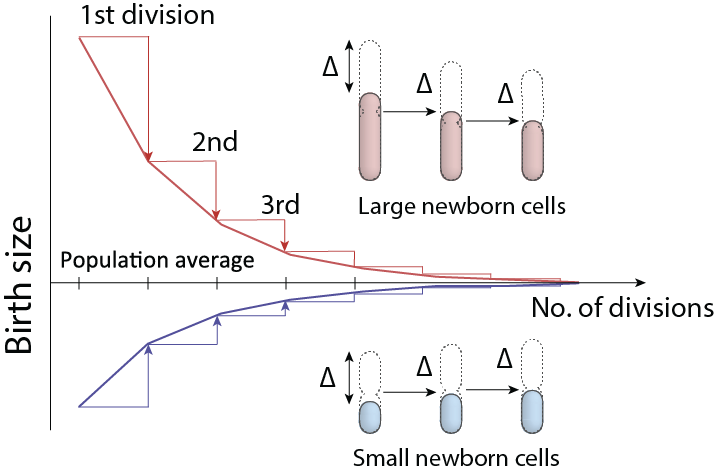
-
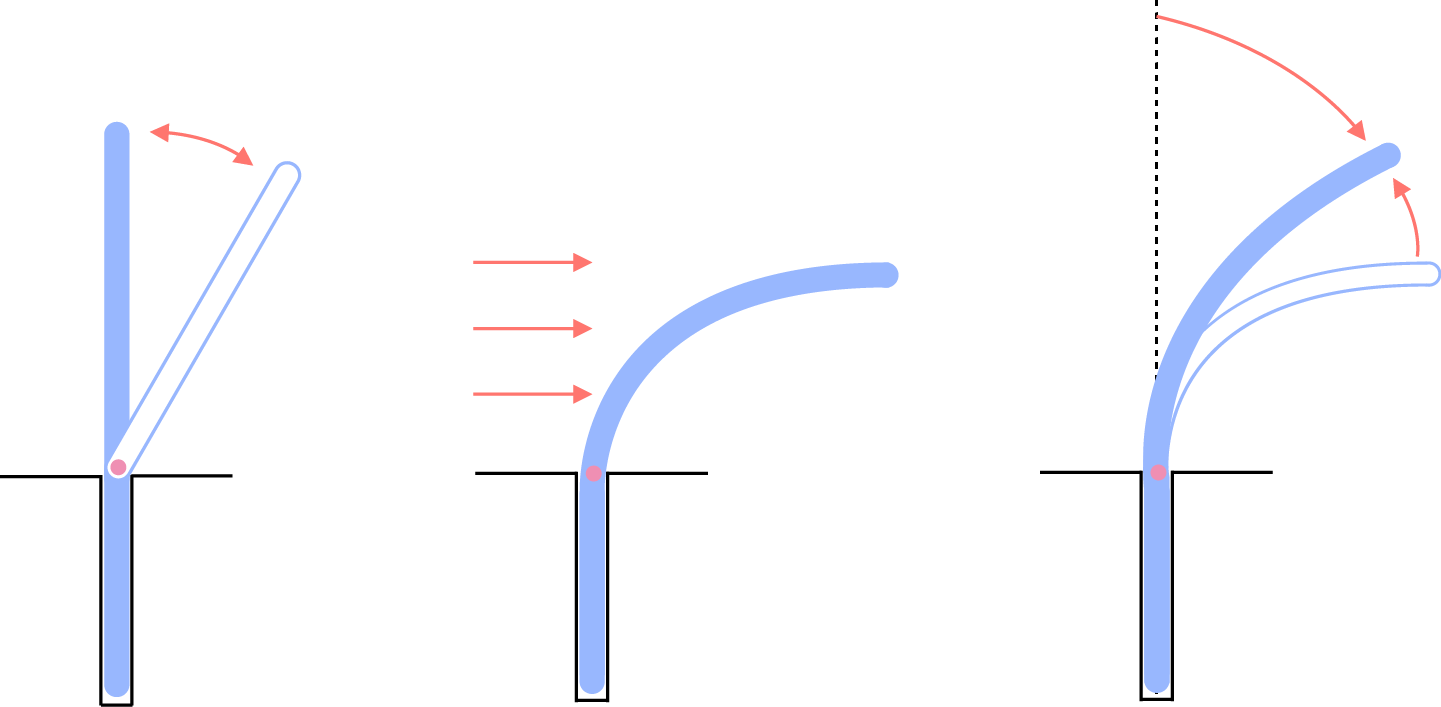
Growth as the origin of morphological plasticity
A. Amir, F. Babaeipour, D. B. McIntosh, D. R. Nelson, S. Jun, PNAS 111, 5778–5783 (2014).
This was originally a summer project for three interns in our previous lab at Harvard in 2009. We noticed that cells growing in the mother machine always bend during growth by the growth media flow, and do not recover their shape immediately even if the flow stops. However, when we repeated the experiments in water, thus without growth, cells bend like an elastic rod and recovers the original straight shape completely and immediately. We concluded that it is growth that is the origin of morphological plasticity of E. coli.
The pioneering interns playing ping pong in 2009: Emily Hanna (front left) and Alyssa Kanagaki (front right) were summer undergrad research students from Barry University and Hamilton College, respectively, and Christina Nürnberg (ping pong master) was a 12th grade of the Erzbischöfliche Gymnasium in Germany.

Read more -
Chromosome organization during overlapping cell cycles
AB. Youngren, H. Nielsen, S. Jun, S. Austin, Genes & Development 28, 71–84 (2014).
This work by Stuart Austin’s group is the first to crack the organization of the E. coli chromosome including replisome positions during multifork replication. The results are consistent with the entropic spring view of the E. coli chromosome.
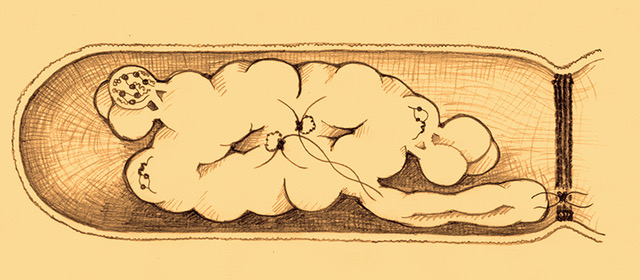
Read more -
Bacterial chromosome as a “soft” entropic spring
J. Pelletier et al., PNAS 109, E2649–56 (2012)
We originally developed the “mother machine” to do the experiments presented in this paper. Our idea was to build an artificial cell-like environment, confine ex vivo bacterial chromosomes, and physically and biochemically manipulate them. Eventually, our dream was to replicate the ex vivo chromosomes. This work presents novel, extensive experimental and theoretical results that show bacterial chromosomes behave as soft entropic springs. This work took 7 years from its conception to publication.
Read more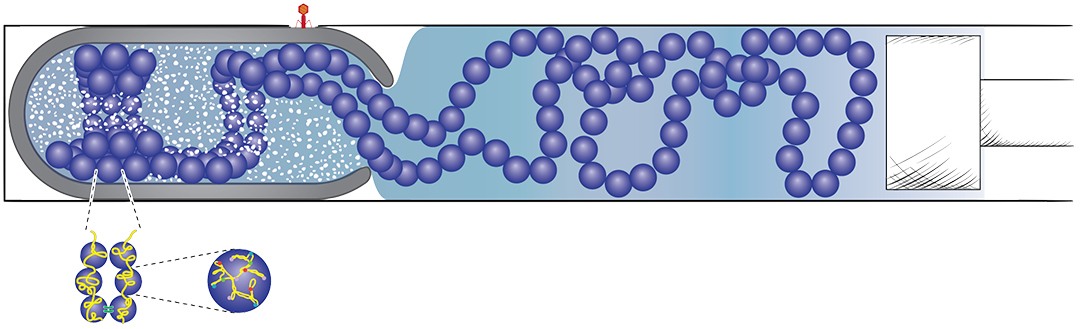
Invention of the Micro-piston
J. Pelletier et al., PNAS 109, E2649–56 (2012)
In the “mother machine”, we compressed and un-compressed individual ex vivo E. coli chromosomes. We used micro beads as a “piston” by manipulating it using optical tweezers. See movie below.
-
E. coli growth is robust and does not show aging
P. Wang et al., Current Biology 20, 1099–1103 (2010).
Using the mother machine, we analyzed the growth and division patterns of hundreds of thousands E. coli cells from the beginning to their death. The growth rate remained remarkably constant, whereas the death rate increased exponentially (albeit very slowly). This is the first work that shows growth is robust and completely decoupled from death in E. coli. Researchers later discovered similar constant growth without aging in other organisms such as B. subtilis and fission yeast S. pombe.
Read moreInvention of the mother machine
P. Wang et al., Current Biology 20, 1099–1103 (2010).
The mother machine is a simple microfluidic device that is extremely versatile and robust. We originally developed it in 2007 to the “piston” experiment (see above micro-piston 2012). We soon realized that we can use the same device to grow and track thousands of individual mother cells for hundreds of consecutive divisions. The mother machine has been adopted by hundreds of labs from microbiology to systems biology across the world.
-
Entropy-driven segregation of the bacterial chromosome
S. Jun, B. Mulder, PNAS 103, 12388–12393 (2006).
Read moreThis is the theoretical work that proposed bacterial chromosomes segregate mainly driven by entropic forces. In physics, this work contributed to the resurgence of interests in polymers in confined space. In biology, this remains one of the major models in bacterial chromosome segregation with supports from both experiments (in vitro and in vivo) as well as modeling.
Icons made by Vignesh Oviyan and Freepik from Flaticon.